9ツルの折方について
2004.07.07 展開図を山あり谷ありに変更
Tomohiro TACHI
なぜ9ツル?
折り紙初心者にとって、折り紙における基本形というのは重要である。基本形を知っていると、自分で展開図を設計するいわゆる「設計折り紙」を考えなくても、広い範囲の折り紙を折ることができるからである。
その「基本形」のなかでもっとも有名なのは「ツルの基本形」であろう。また、「あやめの基本形」というのも有名であろう。その延長上にあるのが「9ツル」である。
それらの特徴を以下に示す。
| 名称 | 長い角 | 短い角 |
| ツル | 04 | 01 |
| あやめ | 05 | 04 |
| 4ツル | 09 | 04 |
| 4あやめ | 13 | 12 |
| 9ツル | 16 | 09 |
あやめ系は短い角が多く、ツル系は長い角が多いことがわかるだろう。
さて、4ツルまでは折方が簡単である。これは展開図から直接見たとおりに折ることができる。4ツルは折ったことのある方も多いと思う。
しかし、それ以降となるとうまくいかない。何が違うかというと「基本形の角を引っ張っても平面に展開しない」ということである。それゆえ作るときも注意が必要なのだ。
そこでうまく折るための方法を示したい。とおもう。
4ツル
先ずは4ツルの展開図を見る。 (※展開図は最終的な面から見たとして赤山、青谷にしています。逆に描く人のほうが多いです。)
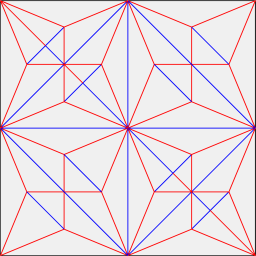
ただし紙の表から見た図
すると、
それぞれの折線が集中した長いかどは凸を○、凹を×であらわすと
○×○
×○×
○×○
のように折られる。ただし、小さい角はすべて凸。
このように凹凸が交互に現れるパターンは折りやすいのである。なぜなら
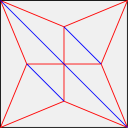
ツルの基本形は
×○
○×
となっていて、この折かただと展開図をつまむだけで折りあがるのだが、4ツルはツルの基本形を凹凸も含めてならべたものだからである
これがまた、角を引っ張って展開できる所以でもある。
9ツルの問題点
さて、これが9ツルの展開図である。

これは
○×○×
×○×○
○×○×
×○×○
とおりたいところである。こう折れば先ほど述べた「ツルの基本形を凹凸も含めてならべたもの」にあたるからである。しかし
○×○×
×○?○
○?○×
×○×○
?で示した部分を凹で折るとこちらから見たのと反対の色の角が出来上がってしまうという問題が出てくる。そしてまた平面に折りたたむことができない。
実際正しい9ツルは
○××○
×○○×
×○○×
○××○
と折る。こうすれば平面に折りたためる。
しかしすると真中に
○○
○○
というパターンが出る。これだけを単品で作るには
○×
×○
という普通のツルの基本形を作ってから下がった2つの角を上にあげるというやり方でできる。
この形は作ってみるとわかるが、角を引っ張っても平面に展開できない。逆にいえば直接平面からつまんで折ることは不可能であって、一定の手順を追わなければならないということである。
9ツルも同じ構造の部分を持つため同様の現象が起きる。さらに9ツルの場合は周りに余計部分がついており、内側をしぼめたときに、そのあまり部分が立体構造を持ってしまうという問題もある。
これらの問題の適度の解決のための方法の一つの例を以下に示す。
9ツルの折方の例1

のように真中から折り始めて、
○×○?
×○×○
○×○×
?○×○
とおると、?のところが直角二等辺三角形状に飛び出る形で折りたためる。紙は裏が出てくる
折りたたんでから、かどをおしあげて
○×○?
×○○○
○○○×
?○×○
として、
○××○
×○○×
×○○×
○××○
とやります。
これは非常にシンプルでわかりやすい。がしかし、これはかなり急激に膨らんでいる角をつぶすので紙に対する負荷が大きい。薄い和紙のようにやわらかい紙でやる場合には良いかもしれないが、ほかの場合は現実的ではない。ただし、これがあと二つの折方の考え方の基礎となる。
9ツルの折方の例2

のように
○×??
×○×?
?×○×
??×○
としてから
かどをおしあげて
○××?
×○○×
×○○×
?××○
として、
○××○
×○○×
×○○×
○××○
とやればよろしい。
この場合はある程度普通の紙でも折れる。ただまだ、紙に良くない力を与えることは事実である。
9ツルの折方の例3

のように
○×??
×○??
??○×
??×○
とおる。
○×??
×○○?
?○○×
??×○
として、ここで、すこし複雑な折方をして
○××?
×○○×
×○○×
?××○
とsr。
○××○
×○○×
×○○×
○××○
これは、紙に対する負担は少なめだが結構難しい。なぜかというと
○○
××
が難しいからである。これは次のように折る。

まとめ
○×
×○
は折りやすいパターンであり展開しやすい。
○○
○○
はいったん上のパターンを作ってから下がった角をおりあげる。
○○
××
は小さい角を長い角のどれかの間にはさむことによって、一番上のパターンから生成される。
応用
結局9ツルはこんな形である。

そして9ツルを使って折った作品である。

飛び立つクワガタムシ。








