蛇腹には任意の長さの角を好きな位置に出せるという特性ほかに、幅を変更したり二次元的に角の位置を調整したり、さまざまな折り返しのパターンを違うパターンと繋げられるという特徴がある。 この特徴を積極的に利用すれば、蛇腹が敬遠されがちである理由の一つの「針金のような形になり作品のイメージと合わない」という問題を解決するだけでなく、蛇腹と繋がる立体造型における裏領域の位置の平行移動などが可能となる。 既にさまざまな蛇腹による造型に使われていおり多くの可能性を持っているパターンといえる。
蛇腹の異種のパターンの複合を取り入れた作品としては神谷哲史氏の龍神が挙げられる。 龍神の鱗のパターン(2:1)と全体を構成するいわゆる通常の蛇腹パターン(1:1)のつながりがこの作品において重要な役割を果たしている。
蛇腹において任意の長さの角を好きな位置に出す設計をする方法は帯領域ジャバラ法として目黒俊幸氏が提唱している。(「ようこそ折り紙のページへ」掲示板の[651]より始まる「ジャバラ系折線構成のための折紙設計システム」)。
そこで蛇腹の異種パターン組み合わせの方法を簡単に設計できるよう帯領域ジャバラ法と合わせて使うための方法を示したい。と思う。
帯領域ジャバラ法においては「等高数」という概念が用いられる。
等高数は展開図を畳んだとき横分子の作る角の向く方向に対して垂直な方向の座標の値である。
展開図上では、蛇腹の折線に沿って一定であり、帯領域の縁にそっては10101と交互にくりかえす数値である(図1)。
帯領域ジャバラ法においてコントロール可能なのは横分子の長さ及び、その方向での位置のみでありそれに垂直な方向のコントロールすなわち等高数の自由な設計はできない。
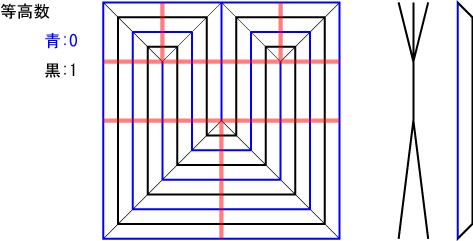 図1
図1
ここで畳んだ形を90°回転させれば、等高数の方向に角の位置と長さをとり、いままで角の位置や長さをあらわしていたほうを等高数として考えることができる(図2)。 すなわち、等高数は畳んだ形に関して直行する方向に二種類取ることができ、蛇腹線に沿って一定であり横分子のまわりを10101と繰り返す数値(以下縦等高数)と帯領域の境界に沿って一定であり蛇腹線に沿って動くと値が大きくなる数(以下横等高数)の二種類を考えることが出来る。(図3)。
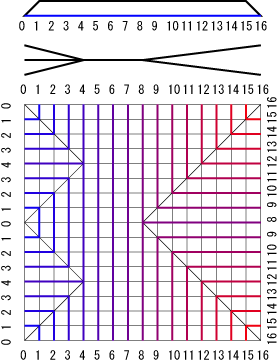 図2
図2 図3
図3こうすることによって二つの形状が90°折れ曲がった形でくっつくこととなる。
実際のところAとBというパーツに分けたときAの横等高数がBの縦等高数になり、Aの縦等高数がBの横等高数となるようなパターンをつなげれば(一方が一定でなくても)90°に折れた状態で新しい形状が繋がる。
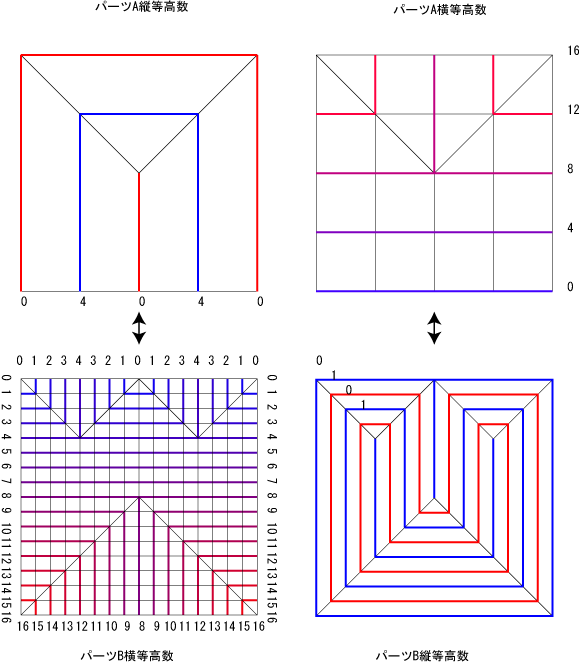 図4
図4
応用例の図解したものもそのうちまとめようと思っています。
直角になってしまうのが具合悪いときは二回連続で使えば同じ方向で変更できる。
立体折や模様折りなどに由来する部分的な蛇腹をずらして他のパーツと組み合わさるようにしたパターンを容易に設計できる。
図4で示した図は幅を変更する例となっている。
二つの帯領域を交差させることで平面を作ることが可能
方形領域であらわされる角の根元の折り倒し方によって横等高数が増える方向に向かう場合と減る方向に向かう場合がある。これを上手く利用すれば効率よくパターンの変換を行える。